Mechanistic modelling

Mechanistic modelling#

This notebook introduces the concept of mechanistic modeling in chemical and biochemical engineering, discussing key principles, types of models, and presenting a simple example of a mechanistic model for a reaction process.

1. Introduction to Mechanistic Modeling#

Mechanistic modeling involves constructing mathematical models based on the fundamental physical, chemical, or biological principles governing a system. These models rely on conservation laws, such as mass, energy, and momentum balances, along with reaction kinetics and transport phenomena.

Mechanistic models are widely used in chemical and biochemical engineering to simulate and optimize processes like:

  • Chemical reactions (e.g., batch reactors)

  • Bioreactors (e.g., microbial growth)

  • Transport phenomena (e.g., heat and mass transfer)

In these models, parameters have physical meaning, and equations are derived from the underlying processes.

2. Key Concepts in Mechanistic Modeling#

The following principles form the foundation of mechanistic models:

  1. Conservation Laws:

  • Mass balance: Input - Output + Generation - Consumption = Accumulation

  • Energy balance: Energy in - Energy out + Heat generated = Accumulation

  • Momentum balance: Force = Mass × Acceleration (Newton’s law)

  1. Reaction Kinetics:

  • Rate equations describe the speed of reactions, which are crucial for modeling chemical processes.

  1. Transport Phenomena:

  • Modeling the movement of mass, energy, and momentum is essential for process design and optimization.

3. Example: Modeling a Simple Chemical Reaction#

Let’s model a simple irreversible first-order reaction in a batch reactor, where the species A is converted to species B:

𝐴 → 𝐵

The rate of the reaction is given by: $\( r_A = -k * C_A \)$ Where:

  • \(C_A\) is the concentration of species A (mol/L)

  • k is the reaction rate constant (1/s)

The mass balance for species A in the reactor is:

\[ \dfrac{C_A}{dt} = -k C_A \]

Analytical solution

The analytical solution for the concentration of 𝐴 over time is: $\( C_A(t) = C_{A0}*e^{-kt} \)\( where \)C_A0$ is the initial concentration of A ​

4. Python example: solving reaction kinetics#

We will use Python to simulate the concentration of species A over time for a giiven initial concentration \(C_{A0}\) and rate constant k.

# Import necessary libraries
import numpy as np
import matplotlib.pyplot as plt

# Reaction rate constant (1/s)
k = 0.1  # Assume k = 0.1 1/s

# Initial concentration of A (mol/L)
C_A0 = 1.0  # mol/L

# Time points (s)
time = np.linspace(0, 50, 500)

# Analytical solution for concentration of A over time
C_A = C_A0 * np.exp(-k * time)

# Plotting the concentration of A over time
plt.figure(figsize=(8, 5))
plt.plot(time, C_A, label='Concentration of A', color='b')
plt.title('Concentration of A vs Time for a First-Order Reaction')
plt.xlabel('Time (s)')
plt.ylabel('Concentration of A (mol/L)')
plt.grid(True)
plt.legend()
plt.show()
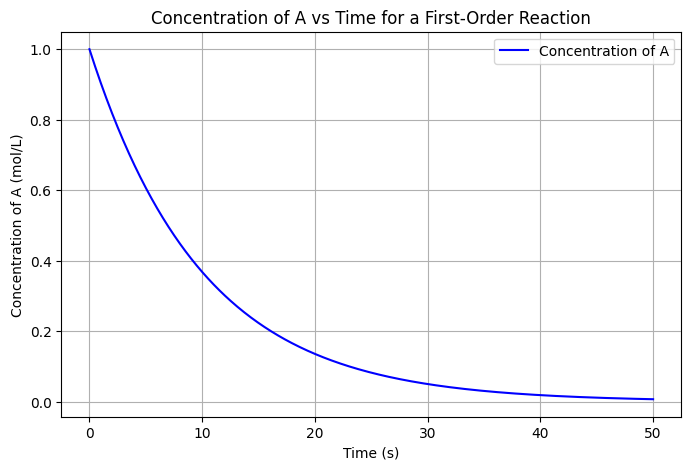
../../_images/b3bdcd6ea56b103e5d6d9f5d6ac7fdd4d7628cb7e0f8a8e63810fd8f83a3810d.png

The graph shows that the concentration of 𝐴 decreases exponentially over time due to the first-order reaction. As time progresses, more of species A is converted to species 𝐵, following the reaction kinetics.

5. Mechanistic Modeling in Biochemical Engineering#

In biochemical engineering, mechanistic models are used to describe processes like microbial growth, enzyme kinetics, and bioreactor performance.

Example: Monod Kinetics for Microbial Growth Microbial growth in a bioreactor can be modeled using Monod kinetics, where the growth rate depends on substrate concentration: $\( \mu = \mu_{mx} \frac{S}{K-S + S} \)$ where:

  • \(\mu\) is the specific growth rate

  • \(\mu_{max}\) is the maximum growth rate

  • S is the subtrate concentration

  • \(K_S\) is the half-saturation constant The jicrobial growth is described in abioreactor as below with X being the biomass concetration $\( \dfrac{dX}{dt} = \mu X \)$

6. Conclusion#

Mechanistic modeling in chemical and biochemical engineering provides valuable insights into system behavior, allowing engineers to predict performance, design optimal processes, and improve operational efficiency. The use of mathematical models based on fundamental principles makes mechanistic modeling a powerful tool in process engineering.

Contents